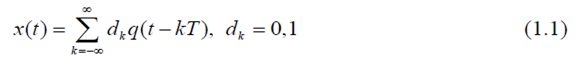What is Duobinary Modulation for Optical Systems?
>> Why NRZ Isn’t Always the Best Modulation Format
Most optical systems use NRZ modulation format. While NRZ modulation is suitable for long haul systems in which the dispersion of the single mode fiber is compensated for by another fiber with negative dispersion, it is not the best choice for uncompensated single mode fibers.
Duobinary modulation turns out to be a much better choice in this case, since it is more resilient to dispersion and is also reasonably simple to implement.
We will explain the basics of duobinary modulation and present the lab test result which shows that duobinary modulation is much more better than NRZ modulation for the uncompensated optical fiber channel.
>> The Basics of Duobinary Modulation
Simply put, duobinary modulation is a method for transmitting R bits/second using less than R/2 Hz of bandwidth.
However, the most famous theory of communication – the Nyquist’s sampling theorem, shows that in order to transmit R bits/second with no intersymbol interference, the minimum bandwidth required of the transmitted pulse is R/2 Hz. This means that duobinary pulses will have ISI (Intersymbol Interference).
However, this ISI is introduced in a controlled manner so that it can be subtracted out to recover the original values.
Let the transmitted signal be
Here {dk} are the data bits, q(t) is the transmitted pulse, and T=1/R is the bit period.
The pulse q(t) is usually chosen such that there is no ISI at the sampling instances (t=KT, k=0,+/-1, …, are the sampling instances):
NRZ is one such scheme and requires a bandwidth of R Hz to transmit R bits/second (this is twice as large as the Nyquist bandwidth of R/2 Hz).
The simplest duobinary scheme transmits pulses with ISI as follows:
We then see from (1.1) and (1.3) that at the sampling instance kT, the receiver does not recover that data bit dk, but rather (dk-1 + dk). However, this scheme allows for pulses with a smaller bandwidth. By allowing some ISI, the transmitted pulse q(t) can be made longer in the time domain, and hence its spectrum becomes narrower in the frequency domain. With a narrower spectrum, the distortion effects of the channel are also fewer. This outcome is one of the reasons why duobinary modulation is resilient to dispersion.
One way of generating duobinary signals is to digitally filter the data bits with a two-tap finite impulse response (FIR) filter with equal weights and then low-pass filter the resulting signal to obtain the analog waveform with the property in (1.3) as shown in figure 1a below.
When the input to the FIR filter is binary (let these binary values be –1 and 1), the output can take on one of three values: 0.5*(-1+(-1))=-1; -1+1=0; or 0.5*(1+1)=1. Hence the duobinary signal is a three level signal.
An important property of the three-value sequence at the output of the FIR filter is that it is a correlated signal and hence all possible sequences of the three values cannot occur. For example, the output sequence of the FIR filter cannot contain a 1 followed by a –1, or a –1 followed by a 1; a 1 and a –1 will always have a 0 between them.
Similarly, the combinations {1 0 1} and {-1 0 –1} also can never occur at the output of the FIR filter; only a {-1 0 1} or a {1 0 –1} can occur. As will be explained later, this sequence is another reason why duobinary modulation is resilient to dispersion.
On a final note, the FIR filter and the low-pass filter can be combined into a single analog filter for ease of implementation (as shown in figure 1b). The two-tap FIR filter is after all a simple low-pass digital filter. For a 10Gbps data stream, a good filter that combines the functions of the FIR filter and the analog filter is a 2.8GHz Bessel filter.
>> Differential Encoding
The ISI introduced at the transmitter can be unraveled at the receiver by differential encoding. At each sampling instance kT, the receiver assumes the value of xk = (dk + dk-1), where xk = x(kT) and x(t) satisfies (1.3). If the precious decision at the output of the receiver is ![]() , this decision can be subtracted from the sampled value to obtain
, this decision can be subtracted from the sampled value to obtain ![]() :
:
However, a single error at the receiver will propagate forever, causing a catastrophic decoding error. To avoid this catastrophic error propagation, it is better to move this differential decoding to the transmitter and differentially precode the data.
The data bits dk are differentially encoded as follows:
The transmitted signal is now
with q(t) satisfying (1.3). Hence at the sampling instance kT, the receiver samples the value ![]() .
.
>> Implementing a High-Speed Differential Encoder
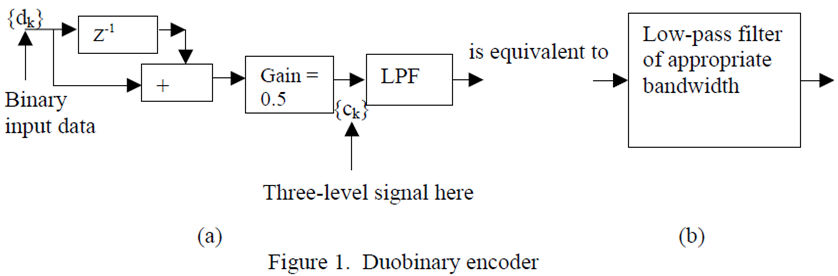
One circuit that can be used to implement a differential encoder is an exclusive-OR (XOR) gate as shown in figure 2 below. However, it can be difficult to implement the 1-bit delay in the feedback path at high data rates such as 10 Gbps.
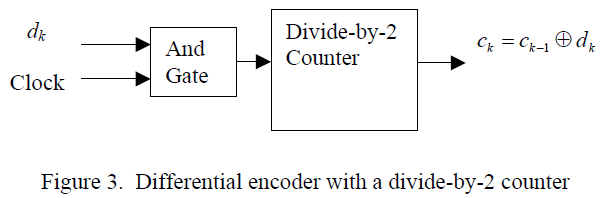
Another circuit that does not involve delay in the feedback path is shown in figure 3 below. Here, a divide-by-2 counter has a clock gated with the data. When the data is high, the counter changes state, which is equivalent to adding a 1 modulo 2. When the data is low, the counter state remains the same, which is equivalent to adding a 0 modulo 2.
>> The Optical System
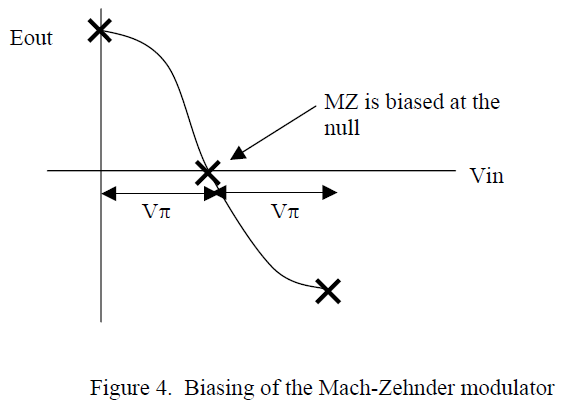
The final step is to modulate the light with the three-level duobinary signal, which implies a three-level optical signal. This result is achieved with a Mach-Zehnder (MZ) modulator biased at its null point. With a zero input, no light is transmitted, but the +1 and –1 inputs are transmitted as +E and –E electric fields.
While this is a three-level signal in terms of the electric field, it is a two-level signal in terms of optical power. This choice significantly reduces the complexity of the receiver (the first optical duobinary systems used a mapping that requires three levels of optical power).
One of the key components is a driver that can produce a voltage swing of 2*Vπ volts at high data rates such as 10 Gbps in order to drive the MZ modulator.
The combination of the duobinary encoder and the above mapping to electric fields helps further reduce the effects of dispersion in the fiber. As the pulses travel down the fiber, they spread out in time owing to dispersion. In an NRZ scheme, a data sequence of {1 0 1} is mapping onto the optical domain as {+E 0 +E}. In the encoded duobinary sequence, a {1 0 1} sequence cannot occur, but a {1 0 –1} does occur, which is mapped to {+E 0 –E} in the optical domain. The effect of dispersion in the two cases is shown in figure 5 below, which depicts why the resulting dispersion is less in the case of duobinary modulation.
The same receiver that is used for a NRZ modulation scheme can be used for duobinary modulation. The power detector squares the electric field to detect power and hence the +E and –E outputs of the fiber get mapped to the same power level and are detected as logical 1s.
>> The Complete Duobinary Transmitter
The complete duobinary transmitter is shown in Figure 6 below. An inverter is added at the input to the differential encoder; without it, the data at the receiver is inverted. This inverter can be placed either at the receiver or the transmitter. Since signal paths are usually differential, the inverter is not an additional piece of hardware that is required but instead can be implemented by reversing the differential lines from the data source to the AND gate. The exact sequence of transformations that occur in the data path at each stage is given in an example in Figure 7.
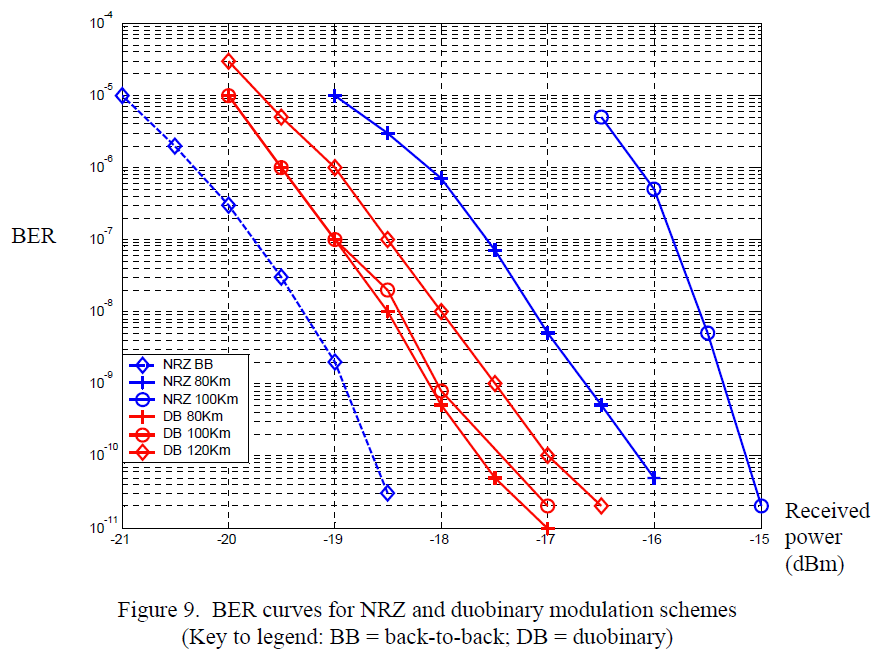
>> Lab Test Result
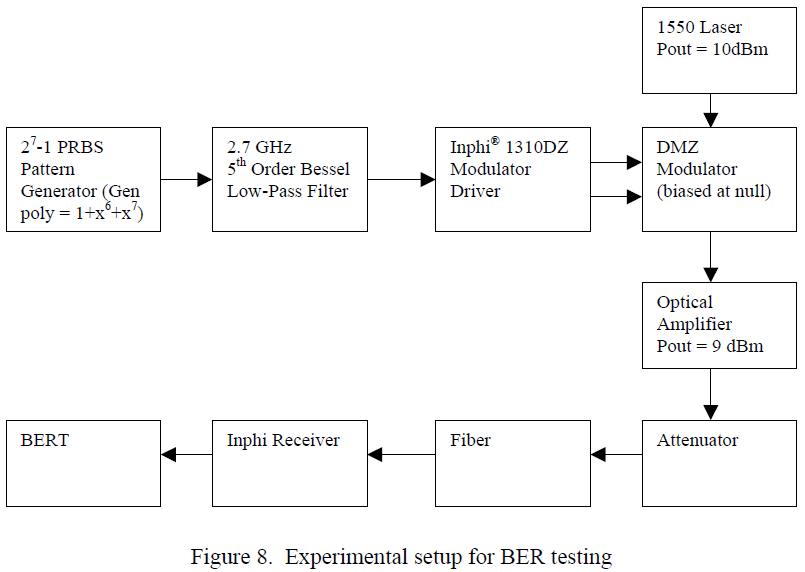
Measurements were carried out to determine the performance of duobinary modulation and compare it with that of NRZ modulation at 10 Gbps. The measurements were made at 1550nm over standard single mode fiber (SMF). This fiber has a dispersion of 17 ps/nm*km at this wavelength and an attenuation of 0.2 dB/km. The experimental setup is depicted in Figure 8. An optical amplifier was added after the MZ modulator to compensate for the loss in the MZ modulator and to launch sufficient power to transmit through 120km of fiber. The power launched into the fiber was kept as a level low enough to avoid any self-phase modulation effects.
An interesting property of the 27-1 PRBS sequence used (generator polynomial = 1 + x6 + x7) is that following differential encoding, it is the same PRBS sequence shifted by 6 bits. (The property that a differential encoded PRBS sequence is a delayed version of the original sequence holds true whenever the generator polynomial is of the form 1 + xn + xn+1, n > 0, and the resulting delay between the PRBS sequence and the differential encoded sequence is (n-1)). Since the BERT is capable of aligning the transmitted and received data streams, the delay is of no consequence, and the step of differential encoding the data can be eliminated.
>> What This Tells Us
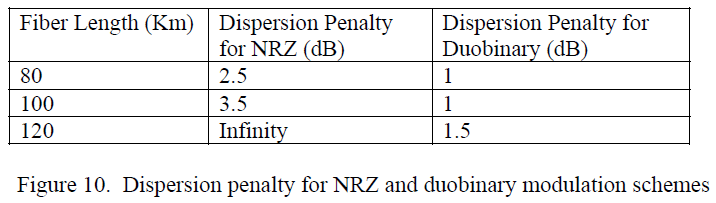
Duobinary modulation is a much more resilient modulation scheme compared with NRZ modulation in the presence of chromatic dispersion. It is possible to extend the reach of NRZ systems from 80km to 120km without the use of dispersion compensating fibers. While a NRZ system is dispersion limited at 120km, a duobinary system is power limited at this same 120km length of SMF fiber. The components are available today to implement such systems.