Optical Fiber Dispersion
1. Light Pulse Dispersion and the Reasons
In digital communication systems, information is encoded in the form of pulses and then these light pulses are transmitted from the transmitter to the receiver. The larger the number of pulses that can be sent per unit time and still be resolvable at the receiver end, the larger is the capacity of the system.
However, when the light pulses travel down the fiber, the pulses spread out, and this phenomenon is called Pulse Dispersion. Pulse dispersion is shown in the following figure.
Pulse dispersion is one of the two most important factors that limit a fiber’s capacity (the other is fiber’s losses). Pulse dispersion happens because of four main reasons:
A) Intermodal Dispersion (also called Modal Dispersion or Group Delay)
Modal dispersion is only important in multimode fibers.
Many different modes propagate in a multimode fiber. Each of these modes takes a different path and thus different length when traveling down the fiber.
Another factor is the differing propagation constants associated with each mode (each mode’s group velocity).
Both factors contribute to modal dispersion.
Single mode fiber doesn’t have modal dispersion since there is only one mode propagating in the fiber. As we shall see, single mode fiber’s bandwidth is mainly limited by material dispersion, waveguide dispersion and PMD (polarization mode dispersion).
B) Material Dispersion (also called Chromatic Dispersion)
Material dispersion is caused by the velocity of light (or its refractive index) being a function of wavelength. Each wavelength takes different amounts of time to propagate the same path.
The following figure shows refractive index versus wavelength in silica.
Any given light source (even a laser) emits over a range of wavelengths as shown below.
C) Waveguide Dispersion
Waveguide dispersion is a type of dispersion attributable to the relationship of the physical dimensions of the waveguide and the optical signal.
In optical fibers, this shows as the propagation constant of a mode (and, hence, its velocity) being a function of a/λ. Where a is the core radius and λ is the wavelength.
Unlike material dispersion, even if the refractive indexes of the core and cladding are independent of wavelength, we will still have waveguide dispersion.
C) Polarization Mode Dispersion (PMD)
PMD is only important in single mode fibers.
In single mode fiber, only one mode can propagate. This mode is actually composed of two distinct polarization modes. The electric fields of the two modes are perpendicular to each other. As shown below.
These two polarization modes are identical in a perfectly symmetrical fiber. However, in reality there is no perfect optical fiber. Stresses within the fiber, and forces applied to it from the outside world, causes the refractive index of glass (thus velocity) to differ very slightly for light in the two polarization modes. Thus these two polarization modes arrive at slightly different time at the end of the fiber. This is called Polarization Mode Dispersion (PMD) and is shown below.
Polarization Mode Dispersion is smaller in magnitude than material dispersion, so it hasn’t been a problem until recently high speed long distance single mode fiber systems becomes popular. PMD is a serious problem when data rate exceeds 2.5 Gb/s.
2. Modal Dispersion
A. Step-Index Multimode Fiber Modal Dispersion
Here we stress that the following analysis uses ray optics. Ray optics modal analysis is only valid when the V number is greater than 10. If the V number is lower, wave theory has to be used.
In a step-index multimode fiber, the center ray with a 0° incident angle travels fastest straight down the fiber. The ray which is incident at the critical angle travels slowest. The time delay between these two modes is given by
 where n1 is refractive index of the core, n2 is refractive index of the cladding, L is the length of the fiber, V is the V number given by
where n1 is refractive index of the core, n2 is refractive index of the cladding, L is the length of the fiber, V is the V number given by

![image_thumb4[1] image_thumb4[1]](https://s3-us-west-1.amazonaws.com/foscoshopify/graphics/uploads/2010/09/image_thumb41_thumb.png) here a is the core radius, λ is the light’s vacuum wavelength.
here a is the core radius, λ is the light’s vacuum wavelength.
Example:
Consider a step-index multimode fiber with a 50um diameter core, 125um diameter cladding, n1 = 1.47, △ = 1.5%. Calculate the modal dispersion in units of ns*km-1 for this fiber at 850nm wavelength.
From above formula, we get
B. Graded-Index Multimode Fiber Modal Dispersion
In grade-index profile multimode fiber, the modal dispersion calculation becomes a little more complicated since we have to account for the inhomogeneous velocity of the light in the fiber as well as the sinusoidal paths as shown above.
Although the higher-order modes need to travel longer path lengths, their average velocity is also higher than the light ray at the center (graded-index fiber has highest refractive index at the center and then gradually decreases toward the cladding).
Here we just give out the conclusion of graded-index multimode fiber modal dispersion.
The delay time incurred by the m-th mode of the fiber will be given by
The information on d△/dλ and dn1/dλ is material-dependent and wavelength-dependent and would have to be provided from a study of the materials used in fabrication of the fibers.
From the first equation, if the profile index g is set to an optimum value gopt, the linear term in △ can be eliminated. gopt is given by
From above discussion, we know that graded-index fiber with a optimum index profile gopt can minimize the time delay of the modes. The net delay from the lowest-order modes to the highest order modes is given by
 From this equation, net modal delay can be positive or negative depending on the size of g relative to gopt. For negative modal delay, it means the higher-order modes arrive before the lower-order modes.
From this equation, net modal delay can be positive or negative depending on the size of g relative to gopt. For negative modal delay, it means the higher-order modes arrive before the lower-order modes.
From the comparison of step-index fiber and graded-index fiber modal delay, we know that graded-index fiber modal dispersion is smaller than that of step-index fiber. This is one of the primary advantages of the graded-index multimode fiber over a step-index multimode fiber of the same size.
Current total dispersion values in graded-index multimode fiber is in the order of 0.2ns*km-1 for laser light sources and 1.0 ns*km-1 for LED light sources.
3. Material Dispersion
The above figure shows the variation of refractive index n with wavelength λ for fused silica used in current glass fibers. Material dispersion is caused by the velocity of light (or refractive index) being a function of wavelength as shown above.
All light sources (even a laser source) have some degree of spectral width. This means that even in a single mode fiber (since laser source also has some spectral linewidth), longer wavelengths travel faster and arrive earlier than shorter wavelengths at the receiver, and this causes pulse spreading.
When a temporal pulse propagates through a homogeneous medium, its group velocity vg is given by
 Thus, the time taken by a pulse to traverse length L of fiber is given by
Thus, the time taken by a pulse to traverse length L of fiber is given by
which is dependent on the wavelength λ. The quantity
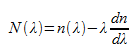 is also referred to as the group refractive index since c/N(λ) gives the group velocity.
is also referred to as the group refractive index since c/N(λ) gives the group velocity.
If the source is characterized by spectral width △λ, then each wavelength component will traverse with a different group velocity, resulting in temporal broadening of the pulse. This broadening is given by
![]() The quantity (λ2d2n/dλ2) is a dimensionless quantity. The above pulse broadening is referred to as material dispersion and occurs when a pulse propagates through any dispersive medium.
The quantity (λ2d2n/dλ2) is a dimensionless quantity. The above pulse broadening is referred to as material dispersion and occurs when a pulse propagates through any dispersive medium.
Material dispersion Dm is usually specified in units of picoseconds per kilometer (fiber length) per nanometer (spectral width of the source) as given by
![]() where λ is in micrometers (um).
where λ is in micrometers (um).
The quantity (λ2d2n/dλ2) characterizes the material dispersion of the fiber and is grouped in the equation. Here is the plot of (λ2d2n/dλ2) for fused silica (the material for current glass fibers).
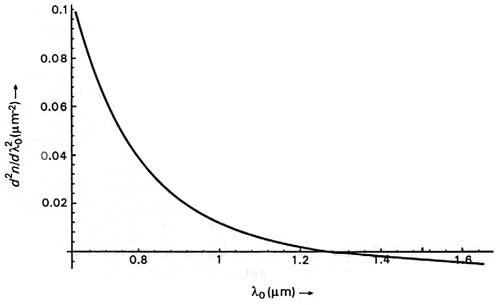 From the above figure, we can see that with λ ≈ 1.27um, d2n/dλ2 ≈ 0. This means that at λ ≈ 1.27um the material dispersion of fused silica changes sign. For λ ≈ 1.27um the material dispersion is zero. This wavelength is referred to as Zero Material Dispersion Wavelength (ZMDW). However, we will see that the other sources of dispersion move the wavelength for zero total dispersion to 1300nm.
From the above figure, we can see that with λ ≈ 1.27um, d2n/dλ2 ≈ 0. This means that at λ ≈ 1.27um the material dispersion of fused silica changes sign. For λ ≈ 1.27um the material dispersion is zero. This wavelength is referred to as Zero Material Dispersion Wavelength (ZMDW). However, we will see that the other sources of dispersion move the wavelength for zero total dispersion to 1300nm.
4. Waveguide Dispersion
As shown in “Basic Optics For Optical Fiber”, for a step-index fiber, when 0 < V < 2.405, the fiber becomes a single mode fiber which means that only one guided mode can propagate in the fiber.
In single mode fiber, there is no Modal Dispersion as discussed above. Pulse spreading (pulse dispersion) happens because of two mechanisms: (1) Material Dispersion as discussed above. (2) Waveguide Dispersion as will be discussed here.
Waveguide dispersion results from the propagation constant of a mode (its group velocity) being a function of a/λ (a is fiber’s core radius, λ is light’s vacuum wavelength). Waveguide dispersion is negligible in multimode fibers and in single mode fibers operated at wavelengths below 1um, but it becomes important for single mode fibers operated in above 1.27um.
The normalized propagation constant b of a mode is defined by
 Since, for guided modes β/k0 lies between n1 and n2, b lies between 0 and 1.
Since, for guided modes β/k0 lies between n1 and n2, b lies between 0 and 1.
For step-index fibers, b depends only on the V value of the fiber, the above equation can be rewritten as
In the above equation, the ≈ step is concluded based on that n1 is very close to n2 which is true for all practical fibers. Thus we can conclude
![]() The group velocity is given by
The group velocity is given by
 In the above equation, n1 and n2 are assumed to be independent of λ.
In the above equation, n1 and n2 are assumed to be independent of λ.
Since
 So the time taken by a pulse to traverse length L of the fiber is given by
So the time taken by a pulse to traverse length L of the fiber is given by
 So for a light source with a spectral width of △λ, the waveguide dispersion is
So for a light source with a spectral width of △λ, the waveguide dispersion is
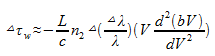 This is our desired expression for the waveguide dispersion.
This is our desired expression for the waveguide dispersion.
For the lowest-order mode(the HE11 mode), our have b(V) as
![]() The following figure shows the variations of b, d(bV)/dV, and V(d2(bV)/dV2) for the fundamental mode as a function of V for a step-index fiber.
The following figure shows the variations of b, d(bV)/dV, and V(d2(bV)/dV2) for the fundamental mode as a function of V for a step-index fiber.
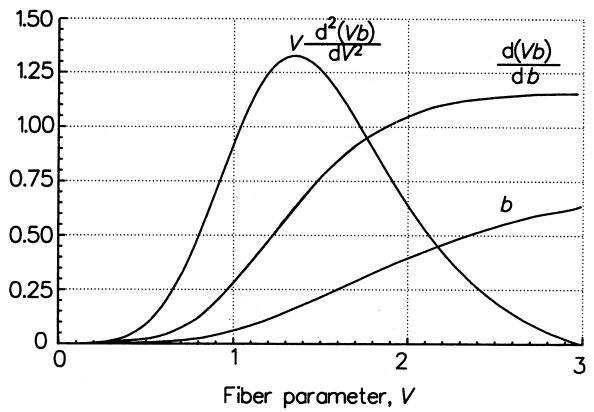 The single mode values of interest are from V = 2.0 to 2.4, as shown below.
The single mode values of interest are from V = 2.0 to 2.4, as shown below.
 In the above figure, the value of V(d2(bV)/dV2) decreases monotonically from 0.64 down to 0.25. Hence in this region, the waveguide dispersion is, in general, a small negative value (because of the minus sign – in the waveguide dispersion expression △τω above).
In the above figure, the value of V(d2(bV)/dV2) decreases monotonically from 0.64 down to 0.25. Hence in this region, the waveguide dispersion is, in general, a small negative value (because of the minus sign – in the waveguide dispersion expression △τω above).
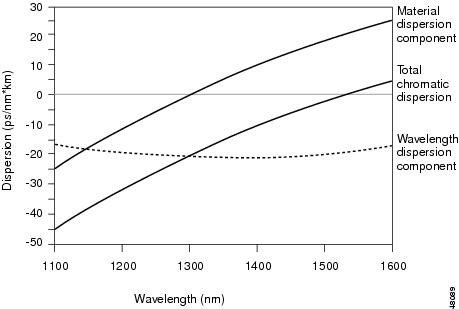
5. Total Dispersion for Single Mode Fiber
It can be seen that the waveguide dispersion is negative in the single mode region. Since the material dispersion is positive for λ greater than the zero material dispersion wavelength, there is a wavelength at which the negative waveguide dispersion will compensate the positive material dispersion. At this wavelength, the net dispersion of the single mode fiber is zero. This is shown below.

Single mode fiber with zero total dispersion around 1300nm is referred to as conventional single mode fiber (CSF) or nondispersion shifted fiber (NDSF). Most installed fiber optic systems today operate with such fibers.
6. Dispersion Shifted Single Mode Fibers
Zero Dispersion-Shifted Fiber (ZDSF)
From the above discussion, we know the conventional single mode fiber has zero total dispersion around 1300nm. However, the minimum fiber loss is at 1550nm. If the zero dispersion wavelength could be shifted to the 1550nm region, we could have both minimum loss and very low dispersion. This would lead to very high bandwidth systems with very long (~100km) repeaterless transmission.
The size of the waveguide dispersion has been found to be sensitive to the doping levels as well as the values of △ and a (core radius). Indeed, we have achieved this by changing the fiber parameters. The resulted fiber is called dispersion-shifted fiber. The first dispersion-shifted fibers had zero dispersion shifted to 1550nm to match their minimum absorption wavelength.
Fiber manufacturers achieved this by adapting the layered core design shown in the following figure.
Although this type of fiber (zero dispersion-shifted fiber) worked well for single channel systems, it proved to be unusable for WDM (wavelength-division multiplexing) systems. When multiple optical channels pass through the same fiber at wavelengths where dispersion is very close to zero, they suffer from a type of crosstalk called four-wave mixing. The degradation is so severe that zero dispersion-shifted fiber cannot be used for dense-WDM systems.
ZDSF were installed in some systems but never came into wide use because of four-wave mixing problem.
Non-Zero Dispersion-Shifted Fiber (NZDSF)
In order to avoid four-wave mixing problem in WDM systems, non-zero dispersion-shifted fibers were invented. The idea is to move the zero-dispersion wavelength outside the band used for erbium-fiber doped amplifiers.
The name Non-Zero Dispersion-Shifted comes from the fact that the dispersion is shifted to a value that is low – but not zero – in the 1550nm bad of erbium-fiber amplifiers. But you can shift the dispersion to a positive or negative value. This small dispersion is enough to keep signals at closely spaced wavelengths from staying in phase over long distances and thus preventing four-wave mixing.
The following figure shows two NZDSF fibers, one with plus sign at 1550nm and one with negative sign at 1550nm (both in light blue color).
Positive dispersion is an advantage because it is easier to compensate than negative dispersion.
This is done by using other layered core structures to adjust the waveguide dispersion differently. The following figure shows two refractive-index profile designs.
Dispersion-Flattened Fiber (DFF)
Another way to minimize dispersion effects for dense-WDM systems is to reduce the slope of the dispersion curve. This is called Dispersion-Flattened Fiber (DFF) as shown in the 3rd figure above in pink color.
The reduced dispersion curve slope helps to simplify the task of dispersion compensation for systems with many optical channels, but there are tradeoffs. An important one is that dispersion-flattened fiber designs tend to have smaller mode-field diameter which concentrate optical power in a smaller volume. The increased power density in fiber can cause non-linear effects.
Dispersion-Compensating Fiber
Now, in many countries, tens of millions of miles of CSF (Conventional Single Mode Fiber with zero dispersion near 1300nm) already exist in the underground ducts operating at 1300nm. One could increase the transmission capacity by operating these fibers at 1550nm and using WDM techniques and optical amplifiers. But, then there will be significant residual (positive) dispersion. On the other hand, replacing these fibers by non-zero dispersion-shifted fibers would involve huge cost.
In recent years, there has been considerable work in upgrading the installed 1300nm optimized fiber links for operation at 1550nm. This is achieved by developing fibers with very large negative dispersion coefficients, a few hundred meters to a kilometer, which can be used to compensate for dispersion over tens of kilometers of the fiber in the link.
These fibers tend to have a high-index difference between core and cladding, and often have a small effective area. The following figure shows the refractive-index profile of one design.


![multimode-fiber-modal-dispersion[1] multimode-fiber-modal-dispersion[1]](https://s3-us-west-1.amazonaws.com/foscoshopify/graphics/uploads/2010/09/multimodefibermodaldispersion1_thumb.gif)