Basic Optics for Optical Fiber
1. Light is an Electromagnetic Wave
Fundamentally, light wave is an electromagnetic wave which is described by Maxwell’s Equations. It is composed of electric and magnetic fields. These two fields are perpendicular to each other and to the direction in which the light travels. This is shown in the following figure.
The electric and magnetic field amplitude varies with time as a sine wave, just like a since function in trigonometry.
Wavelength:
Wavelength is the distance between two nearest amplitude positive peaks. The amplitude rises from 0 to a positive peak, goes through 0, goes to negative peak, then returns back to 0. This is a complete cycle and the distance light travels during this cycle is called a wavelength and is usually represented by the symbol λ. This is shown in the illustration below.
2. Refractive Index
Light travels at 299,792,458 meters per second in vacuum. This is roughly 186,282 miles per second. This speed of light in vacuum is usually denoted by c. But light travels more slowly when it passes through a transparent material. The degree of slowing down depends on the material’s refractive index. Refractive index of a transparent material (denoted by n) is defined as:
n = c / v
where c is the speed of light in vacuum, v is the speed of light (velocity) in this transparent material.
The refractive index of water is 1.33, meaning that light travels 1.33 times as fast in a vacuum than it does in water. The refractive index of air at atmospheric pressure and room temperature is 1.000293, so close to 1.0 that the difference is insignificant.
3. Snell’s Law
Light rays travel in straight lines through optical materials, but light rays bend when they pass through a boundary between two different refractive index materials, such as from air into glass. This phenomenon is called refraction and is shown in the following illustration.
Named after Dutch mathematician Willerbrord Snellius, Snell’s law states that the ratio of the sines of the angles of incidence θ1 and refraction θ2 is equivalent to the ratio of light speed (velocities) in the two materials, or equivalent to the opposite ratio of the refractive index of refraction.
Snell’s law is also written as:
n1sinθ1=n2sinθ2
Where
v = velocity (light speed in material)
n = refractive index
θ1 = angle of incidence
θ2 = angle of refraction
4. Total Internal Reflection and Critical Angle
The illustration above for Snell’s law shows the light ray passing from air (n1=1.000293) into glass (n2≈1.5). But what happens when light passes from glass (higher refractive index) into air (lower refractive index).
According to Snell’s law, the equation becomes
1.5 * sinθ1=1 * sinθ2
So θ2 > θ1
This means that instead of being bent closer to the normal, the light is bent farther from the normal. As shown below.
When incidence angle θ1 increases, θ2 also increases. When θ1 increases to a angle θc , θ2 = 90° (sinθ2=1), the refracted wave just grazes the interface. This angle θc is called the critical angle.
θc = arcsin (n2/n1)
When the incidence angle θ1 is larger than the critical angle θc, Snell’s law indicates that refraction can’t take place. Light cannot get out of the glass if the angle of incidence exceeds the critical angle. What happens is that all light rays are reflected back into the glass as shown above, and this phenomenon is called Total Internal Reflection.
Total Internal Reflection is the optical principle that keeps light confined in optical fibers. (the actual mechanism of light guiding is more complex in modern optical fibers, but this theory is good enough for understanding the principles).
For the glass and air example,
θc = arcsin (1/1.5) = 41.8°
5. Optical Fiber Construction and Light Guiding
Optical fiber (shown below) is comprised of a light-carrying core (higher refractive index) surrounded by a cladding (lower refractive index). This construction traps the light in the core by the principle of Toal Internal Reflection.
Since the fiber core has a higher refractive index, the light in the core is totally reflected at the boundary of the cladding for all light that strikes at greater than the critical angle.
The core and cladding are usually fused silica glass covered by a plastic coating, called the buffer. The buffer protects the glass fiber from physical damage and moisture.
Refractive Index Profile of a Step-Index Fiber
The corresponding refractive index distribution (in the transverse direction) is given by
n( r ) = n1, 0 < r < a (core)
= n2, r > a (cladding)
where r is the cylindrical radial coordinate and a is the radius of the core. Typically, for a step index (multimode) silica fiber,
n1 ≈ 1.48, n2 ≈ 1.46, a ≈ 25um
This following table summarizes some of the typical parameters associated with standard fibers. (the values are representative only). △ is the fractional change in the index of refraction, given by

| Type | core diam. (um) | cladding diam. (um) | △ | Application |
| 8/125 Single Mode | 8 | 125 | 0.1% to 0.2% | long distance, high data rate |
| 50/125 Multimode | 50 | 125 | 1% to 2% | short distance, moderate data rate |
| 62.5/125 Multimode | 62.5 | 125 | 1% to 2% | local area network |
| 100/140 Multimode | 100 | 140 | 1% to 2% | local area network, short distance |
Optical Fiber’s Acceptance Angle and Numerical Aperture
Another way to look at light guiding in a fiber is to measure the fiber’s acceptance angle – the angle over which light rays entering the fiber will be guided along its core. Let’s look at the illustration below.
 It can be seen that a ray that meets the first core-cladding interface at the critical angle. This ray meets the fiber core at an incident angle of α, this incident angle α is defined as the acceptance angle of the fiber.
It can be seen that a ray that meets the first core-cladding interface at the critical angle. This ray meets the fiber core at an incident angle of α, this incident angle α is defined as the acceptance angle of the fiber.
Any light rays incident at the fiber core with an angle greater than α will not be refracted sufficiently to undergo Total Internal Reflection at the core-cladding interface, and therefore, although they will enter the core, they will not be accepted into the fiber for onward transmission.
Acceptance angle is measured in air (refractive index ≈ 1) outside the fiber. The acceptance angle normally is measured as Numerical Aperture (NA), which for light entering a fiber from air is approximately
So for a typical fiber n1 = 1.48, n2 = 1.46, NA = 0.242. This implies the acceptance angle is about 14°.
The amount of light accepted into a fiber is directly proportional to its core cross-sectional area and the square of its numerical aperture. The NA of a fiber is a very important property and essentially determines the efficiency of coupling from a light source to the fiber as well as losses across a misaligned joint in a splice.
To maximize the amount of light accepted it is normal to choose fibers with large core diameter and high NA but, as we will see later in the discussion of modes in optical fiber, these fibers tend to lose most light and have relatively low bandwidths.
6. Waveguide Modes in Step-Index Fibers
Step-index fibers have a refractive index profile as shown in the previous illustration (a step discontinuity in the index of refraction at the core-cladding interface). Step-index fibers are cylindrically symmetric dielectric waveguides and can be modeled and solved for the electromagnetic fields that propagate in the fiber.
Among the modes that can propagate in step-index fibers, there are TE modes (electric field transverse to the propagation direction), TM modes (magnetic field transverse to the propagation direction), and hybrid modes (HEmn and EHmn modes, these modes have electric and magnetic fields along the propagation direction).
For typical fibers used in telecommunication and data communication, the refractive index difference between core and cladding, n1-n2, is so small (~0.002-0.008) that most of the TE, TM, and hybrid modes are degenerate and it is sufficient to use a single notation for all these modes – the LP notation.
An LP mode is referred to as LPlm, where the l and m subscripts are related to the number of radial and azimuthal zeros of a particular mode. The fundamental mode is LP01 mode and it is the only mode that can propagate in a single mode fiber.
The following picture shows the LP modes power distribution pattern.

The V-Number(Normalized Frequency)
The V-Number (or called Normalized Frequency) is defined by
a = radius of fiber core
λ = vacuum wavelength of the light
n1 = refractive index of the core
n2 = refractive index of the cladding
The V-number determines how many modes in the fiber. The following illustration shows the relationship between the normalized modal propagation constant b and V-number.
 On the Y axis, b is the normalized modal propagation constant and is defined by
On the Y axis, b is the normalized modal propagation constant and is defined by
 in the above definition, β is the mode’s propagation constant and k = 2π/λ.
in the above definition, β is the mode’s propagation constant and k = 2π/λ.
The above equation for b is hard to use. For LP modes, the following formulas are used to calculate b for different LPlm modes, to a very good accuracy.
The figure of V-number vs. b (above) was generated using this formula.
The wavelength for which b is zero is called the cutoff wavelength (λcutoff) and can be calculated as
 Wavelengths longer than the cutoff wavelength will not propagate in the fiber. The table below lists the cutoff V number for some LP modes.
Wavelengths longer than the cutoff wavelength will not propagate in the fiber. The table below lists the cutoff V number for some LP modes.
| l = 0 Mode | Vcutoff ( J1(Vcutoff) = 0 ) |
| LP01 | 0 |
| LP02 | 3.8317 |
| LP03 | 7.0156 |
| LP04 | 10.1735 |
7. Number of Modes in a Step-Index Multimode Fiber
As shown in the V-number vs b curve above, we can see that for any value of V larger than 2.405, more than one mode will propagate in the fiber.
The numbers of modes that can propagate in a fiber depends on the fiber’s numerical aperture as well as on its core diameter and the wavelength of the light. When V is far larger than 2.405, (V >> 2.405), the estimate total number of modes N can be calculated as
We can use ray theory to explain the modes in multimode fibers. The lowest-order modes correspond to those rays that strike the core-cladding interface at low, grazing angles, and the highest-order modes correspond to the rays that strike the interface at steepest angles (closest to the critical angle).
 Another simple formula to calculate the modes in multimode fibers (when V >> 2.405) is
Another simple formula to calculate the modes in multimode fibers (when V >> 2.405) is
a = core radius
NA = numerical aperture
For example, for the 100/140um (core/cladding diameter) fiber, with a NA = 0.29, λ = 850nm, N will be about 5731.
8. Power Distribution Between Core and Cladding
In optical fibers, the power is not zero at the core-cladding interface. Some of the power (for a particular mode) is carried in the core and some in the cladding. So we have the following figure to tell the power distribution story in fibers.
The power percentage in the cladding can be found on the left axis, the power percentage in the core can be found on the right axis. As shown, more power will go into the cladding as V number approaches cutoff for any particular mode. Once all power transfers to the cladding, this mode will not propagate in the fiber anymore.
9. Step-Index Single Mode Fiber
From the above power distribution figure, we can see that when V < 2.405, only one mode (the LP01) mode can propagate in the fiber, this is called the single mode operation.
Let’s re-exam the V-number formula,
![]()
Single Mode Fiber Cutoff Wavelength
For a given fiber (n1, n2, a), there is a wavelength λc which makes V = 2.405 (the largest V number to meet single mode operation). This λc is called the single mode fiber’s cutoff wavelength. For wavelengths shorter than λc, more modes will propagate in the fiber and the fiber becomes a multimode fiber instead of single mode.
Let’s take another look at the above power distribution figure. At V=2.405, about 84% of the mode’s power is in the core; while at V=1, only 30% is in the core. When V=2, about 75% of the power is in the core.
Power in the cladding is susceptible to effects from the outside environment which can lead to high losses. So for practical single mode fibers, V number is always kept between 2 and 2.405. However, V number should not be too close to 2.405, since then the cutoff wavelength will be too close to the designed operating wavelength.
10. Mode Field Diameter for Single Mode Fiber
As we can see above (Step-Index Single Mode Fiber), in single mode fibers, a fair amount of power is contained in the cladding outside of the core. This means that the mode field diameter (MFD) for LP01 fundamental mode is larger than the core’s diameter in single mode fiber. Look at the figure below.
The mode field diameter (MFD) specifies the transverse extent of the fundamental modal field. For single mode fibers, the modal field extends far into the cladding and MFD can be very different from core diameter. MFD can be used to to estimate joint losses between two single mode fibers, coupling efficiency, cutoff wavelength, backscattering characteristics, microbending and macrobending losses, and even waveguide dispersion.
However, there are three different ways to define the mode field diameter (MFD) as we will show below.
Near-field rms Mode Field Diameter
If φ2(r) is the transverse modal density profile, then the near-field rms MFD dN is defined by
 The near-field spot size is defined as
The near-field spot size is defined as
Far-field rms Mode Field Diameter
The Petermann-2 spot size is defined by
 Where ψ(r) represents the transverse field pattern of the fiber.
Where ψ(r) represents the transverse field pattern of the fiber.
The far-field rms Mode Field Diameter dF is given by
dF = 2ωP
Gaussian Mode Field Diameter
For conventional single mode fibers operating at 1300nm, the fundamental mode can be accurately represented by a Gaussian function of the form
where ω02 is the spot size.
Gaussian Mode Field Diameter dG (for a modal field having a near Gaussian field distribution) can be defined as the diameter of the mode at 1/e2 intensity points, which is given by
dG = 2ω0
However, this usually leads to a poor approximation. A widely used criterion is to choose the value of ω0 so that the Gaussian beam leads to the maximum launching efficiency of the actual fundamental mode.
For example, for a step-index fiber lying in the range of 0.8 < V < 2.5, the following empirical expression gives a value of ω0 that has an accuracy better than 1%.
If the fiber produces a Gaussian-shaped field, then all three definitions reduce to the same value. But if the field is non-Gaussian (as in dispersion-shifted fibers), or the fiber is non-symmetric (as in polarization maintaining fibers), then the definitions diverge slightly.
Conventional step-index single mode fiber designs produce Gaussian-shaped beams; recent advances in designing dispersion-shifted fibers and dispersion-flattened fibers have produced non-Gaussian beams, resulting in revised definitions of MFD.
11. Multi-Step Single Mode Fibers
The expression for V number that we have been using is valid for the simple step-index profile. Conventional Single Mode Fiber (CSF) such as Corning’s SMF-28e fiber uses the step-index profile. The sheer simplicity of single mode transmission and higher bandwidth makes step-index single mode fiber very attractive to fiber optic communications.
However, simple step-index single mode fiber has its own problem too. This type of fiber’s dispersion is at a minimum at 1310nm, but its attenuation is at minimum at 1550nm (1550nm is the most widely used wavelength for single mode operations).
The best optical amplifiers EDFA (Erbium-Doped Fiber Amplifier) operate at 1530nm to 1610nm which has relative large dispersion for simple step-index fibers. This limitation has led optical fiber manufacturers to design single mode fibers with different index profile to improve its dispersion performance at 1550nm.
We will show some of these index profiles here. Each of these profiles has its own electromagnetic distributions and the value of V at cutoff will be different. We will discuss these fibers in detail in the optical fiber dispersion tutorial.
Conventional Step-Index Single Mode Fiber Refractive Index Profile
Depressed Cladding Refractive Index Profile
 Triangular Refractive Index Profile
Triangular Refractive Index Profile
 Segmented Refractive Index Profile
Segmented Refractive Index Profile
12. Graded-Index Multimode Fibers
Until now, all our discussions are based on step-index profile fibers (both multimode and single mode). But in the early 1970s, communication engineers recognized modal dispersion limited the capacity of large-core step-index multimode fibers. Step-index single mode fibers promised much more capacity, but the light source coupling difficulty prevented their applications because of the tiny core (this was true in the 1970s, but nowadays single mode fiber coupling has become standard practice).
So the engineers developed graded-index multimode fiber to improve modal dispersion performance of multimode fibers. Let’s look at the index profile first.
The above figure shows the refractive index profile of a graded-index multimode fiber with 62.5um core diameter. Notice that the index of refraction is a maximum at the center and tapers off to a minimum value at the edge of the core.
Here is the radial index profile formula.
where
n1 = refractive index at the center
(the fractional change in the refractive index from the center to the edge of the core)
r = radial distance
a = core radius
g = profile parameter (the gradient of the graded-index fiber)
Note that when g = 2, the profile becomes a parabolic profile, g = 1 is a triangular profile, and g = ∞ is a step-index profile.
 Refractive Index Variations for a Power Law Profile for Different Values of g
Refractive Index Variations for a Power Law Profile for Different Values of g
Light Guiding of Graded-Index Multimode Fiber
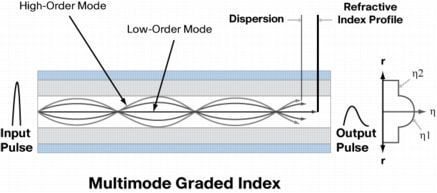
Graded-index multimode fiber does NOT use Total Internal Reflection to guide the light. Instead, it uses refraction. The fiber’s refractive index decreases gradually away from its center, finally dropping to the same value as the cladding at the edge of the core as shown above. The change in refractive index causes refraction, bending light rays back toward the axis as they pass through layers with lower refractive indexes. So the light waves follow a sinusoidal path, as shown below.
How Graded-Index Multimode Fiber Compensates Modal Dispersion
Let’s first exam step-index multimode fibers as shown below. The higher order mode 3 has steeper incident angle and travels a longer path than lower mode 1. Since step-index core has fixed refractive index n1, so all modes travel at the same speed as v = c/n1, where c is the light speed in vacuum. So mode 3 get to the other end of fiber later than mode 1, this is called Modal Dispersion. This is a serious problem in step-index multimode fibers.
Now let’s exam the graded-index multimode fiber below. Higher order mode still travels longer distance than lower mode. However, because of the gradually decreased refractive index from center to the edge of the core, higher mode travels faster than lower mode. (the farther the light goes from the axis of the fiber, the faster its velocity).
The difference isn’t great, but it’s enough to compensate for the longer paths followed by higher modes.
Graded-Index Multimode Fiber Products
Multimode fibers such as Infinicor 300 (62.5um core) and Infinicor 600 (50um core) from Corning are great graded-index profile multimode fiber products.
The standard types have core diameters of 50 or 62.5um and a cladding of 125um. Some manufacturers also make 85um core, 125um cladding products. The core diameters are large enough to collect light efficiently from a variety of light sources such as LED, diode lasers. The cladding must be at least 20um thick to keep light from leaking out.
The graded-index multimode fiber is a compromise and it was used for some telecommunications until the mid-1980s but gradually faded from use in telephone systems because single mode fibers provided much better capacity.
Graded-index multimode fibers are still in popular use but mostly for data communications in short distance, no more than a few kilometers.
Number of Modes in Graded-Index Multimode Fiber
The V number for graded-index fibers (for typically small values of △) is defined in the same way as step-index fibers
![]()
The number of modes N in a graded-index multimode fiber is estimated by








![fiber-mode[1] fiber-mode[1]](https://s3-us-west-1.amazonaws.com/foscoshopify/graphics/uploads/2010/09/fibermode1_thumb.gif)