Optical Fiber Tutorial - Optic Fiber - Communication Fiber
Basic Terms
Refraction of light
As a light ray passes from one transparent medium to another, it changes direction; this phenomenon is called refraction of light. How much that light ray changes its direction depends on the refractive index of the mediums.

Refractive Index
Refractive index is the speed of light in a vacuum (abbreviated c, c=299,792.458km/second) divided by the speed of light in a material (abbreviated v). Refractive index measures how much a material refracts light. Refractive index of a material, abbreviated as n, is defined as
n=c/v
Snell’s Law

In 1621, a Dutch physicist named Willebrord Snell derived the relationship between the different angles of light as it passes from one transparent medium to another. When light passes from one transparent material to another, it bends according to Snell's law which is defined as:
n1sin(θ1) = n2sin(θ2)
where:
n1 is the refractive index of the medium the light is leaving
θ1 is the incident angle between the light beam and the normal (normal is 90° to the interface between two materials)
n2 is the refractive index of the material the light is entering
θ2 is the refractive angle between the light ray and the normal

Note:
For the case of θ1 = 0° (i.e., a ray perpendicular to the interface) the solution is θ2 = 0° regardless of the values of n1 and n2. That means a ray entering a medium perpendicular to the surface is never bent.
The above is also valid for light going from a dense (higher n) to a less dense (lower n) material; the symmetry of Snell's law shows that the same ray paths are applicable in opposite direction.
Total Internal Reflection
When a light ray crosses an interface into a medium with a higher refractive index, it bends towards the normal. Conversely, light traveling cross an interface from a higher refractive index medium to a lower refractive index medium will bend away from the normal.
This has an interesting implication: at some angle, known as the critical angle θc, light traveling from a higher refractive index medium to a lower refractive index medium will be refracted at 90°; in other words, refracted along the interface.
If the light hits the interface at any angle larger than this critical angle, it will not pass through to the second medium at all. Instead, all of it will be reflected back into the first medium, a process known as total internal reflection.
The critical angle can be calculated from Snell's law, putting in an angle of 90° for the angle of the refracted ray θ2. This gives θ1:
![]()
Since
θ2 = 90°
So
sin(θ2) = 1
Then
θc = θ1 = arcsin(n2/n1)
For example, with light trying to emerge from glass with n1=1.5 into air (n2 =1), the critical angle θc is arcsin(1/1.5), or 41.8°.
For any angle of incidence larger than the critical angle, Snell's law will not be able to be solved for the angle of refraction, because it will show that the refracted angle has a sine larger than 1, which is not possible. In that case all the light is totally reflected off the interface, obeying the law of reflection.
How Optical Fiber Works
Optical fibers are based entirely on the principle of total internal reflection. This is explained in the following picture.
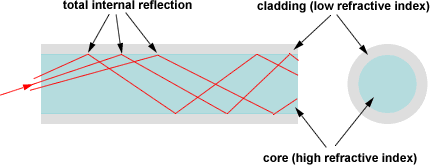
Optical fiber is a long, thin strand of very pure glass about the diameter of a human hair. Optical fibers are arranged in bundles called optical cables and used to transmit light signals over long distances.
The Structure of an Optical Fiber
Typical optical fibers are composed of core, cladding and buffer coating.
The core is the inner part of the fiber, which guides light. The cladding surrounds the core completely. The refractive index of the core is higher than that of the cladding, so light in the core that strikes the boundary with the cladding at an angle shallower than critical angle will be reflected back into the core by total internal reflection.
For the most common optical glass fiber types, which includes 1550nm single mode fibers and 850nm or 1300nm multimode fibers, the core diameter ranges from 8 ~ 62.5 µm. The most common cladding diameter is 125 µm. The material of buffer coating usually is soft or hard plastic such as acrylic, nylon and with diameter ranges from 250 µm to 900 µm. Buffer coating provides mechanical protection and bending flexibility for the fiber.

Optical Fiber Mode
What is Fiber Mode?
An optical fiber guides light waves in distinct patterns called modes. Mode describes the distribution of light energy across the fiber. The precise patterns depend on the wavelength of light transmitted and on the variation in refractive index that shapes the core. In essence, the variations in refractive index create boundary conditions that shape how light waves travel through the fiber, like the walls of a tunnel affect how sounds echo inside.
We can take a look at large-core step-index fibers. Light rays enter the fiber at a range of angles, and rays at different angles can all stably travel down the length of the fiber as long as they hit the core-cladding interface at an angle larger than critical angle. These rays are different modes.
Fibers that carry more than one mode at a specific light wavelength are called multimode fibers. Some fibers have very small diameter core that they can carry only one mode which travels as a straight line at the center of the core. These fibers are single mode fibers. This is illustrated in the following picture.

Optical Fiber Index Profile
Index profile is the refractive index distribution across the core and the cladding of a fiber. Some optical fiber has a step index profile, in which the core has one uniformly distributed index and the cladding has a lower uniformly distributed index. Other optical fiber has a graded index profile, in which refractive index varies gradually as a function of radial distance from the fiber center. Graded-index profiles include power-law index profiles and parabolic index profiles. The following figure shows some common types of index profiles for single mode and multimode fibers.

Optical Fiber’s Numerical Aperture (NA)
Multimode optical fiber will only propagate light that enters the fiber within a certain cone, known as the acceptance cone of the fiber. The half-angle of this cone is called the acceptance angle, θmax. For step-index multimode fiber, the acceptance angle is determined only by the indices of refraction:
![]()
Where
n is the refractive index of the medium light is traveling before entering the fiber
nf is the refractive index of the fiber core
nc is the refractive index of the cladding

How to Calculate Number of Modes in a Fiber?
Modes are sometimes characterized by numbers. Single mode fibers carry only the lowest-order mode, assigned the number 0. Multimode fibers also carry higher-order modes. The number of modes that can propagate in a fiber depends on the fiber’s numerical aperture (or acceptance angle) as well as on its core diameter and the wavelength of the light. For a step-index multimode fiber, the number of such modes, Nm, is approximated by

Where
D is the core diameter
λ is the operating wavelength
NA is the numerical aperture (or acceptance angle)
Note: this formula is only an approximation and does not work for fibers carrying only a few modes.


