A Plain Explanation of Maxwell's Equations
Physical Meanings of Maxwell's Equations
Maxwell's Equations are composed of four equations with each one describes one phenomenon respectively.
Maxwell didn't invent all these equations, but rather he combined the four equations made by Gauss (also Coulomb), Faraday, and Ampere.
But Maxwell added one piece of information into Ampere's law (the 4th equation) - Displacement Current, which makes the equation complete.
- Gauss's law for static electric fields
- Gauss's law for static magnetic fields
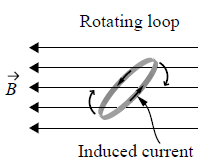
- Faraday's law which says a changing magnetic field (changing with time) produces an electric field
- Ampere-Maxwell's law which says a changing electric field (changing with time) produces a magnetic field
The combination of equations 3 and 4 can explain electromagnetic wave (such as light) which can propagate on its own.
The combination says that a changing magnetic field produces a changing electric field, and this changing electric field produces another changing magnetic field. Thus the cycle continues and an electromagnetic wave is made and propagates through the space.
Mathematical Representations
Maxwell's equations can be expressed in two forms:
- Integral Equations Form
- Differential Equations Form
| Equation Name | Integral Equations Form | |
|
Gauss's Law |
|
|
|
Gauss's Law |
|
|
| Faraday's Law of Induction |
|
|
|
Ampere's Law |
|
| Equation Name |
Differential Equations Form (Point Functions) |
|
|
Gauss's Law |
The electric field produced by electric charge diverges from positive charge and converges upon negative charge. |
|
|
Gauss's Law |
|
|
| Faraday's Law of Induction |
A circulating electric field is produced by a magnetic field that changes with time. |
|
|
Ampere's Law |
A circulating magnetic field is produced by an electric current and by an electric field that changes with time. |
Integral Forms
1. Gauss's Law for Static Electric Fields
 |
 |
| Concepts | Meaning | |
|
Electric Field
|
||
| ◦ |
Dot Product
|
|
|
Unit Normal Vector
|
||
|
|
The Component of E Normal to a Surface
|
|
 |
Surface Integral |
|
 |
The Flux of Electric Field E Over a Surface S
|
|
 |
The Electric Flux Through a Closed Surface
|
|
|
The Enclosed Elctric Charge within the Closed Surface Because any charge located outside the closed surface produces an equal amount of inward (negative) flux and outward (positive) flux, so the net flux is only determined by the charges within the closed surface. If the total enclosed charge is positive, then we have a positive (outward) net flux. If the total enclosed charge is negative, then we have a negative net flux (inward). |
||
|
The Permittivity of Free Space The permittivity of a material determines its response to an applied electric field In dielectric materials, charges do not move freely, but may be slightly displaced from their equilibrium position (called polarization) because the electric field. The permittivity of a medium is a fundamental parameter in determing the speed with which an electromagnetic wave propagates through that medium. ε0 = 8.8541878176 x 10-12 coulombs/(volt-meter) |
2. Gauss's Law for Static Magnetic Fields
 |
 |
| Concepts | Meaning | ||
|
Magnetic Flux Density Also called magnetic field. The magnetic field is defined using the magnetic force experienced by a moving charged particle
|
|||
 |
There are no magnetic monopoles
|
||
 |
The Magnetic Flux Through a Closed Surface Like the electric flux, the magnetic flux through a surface is the "amount" of magnetic field "flowing" through the surface. For a closed surface, the surface penetration is a two-way street: the outward flux is positive, and the inward flux is negative. The net flux is the sum of outward flux and inward flux. |
3. Faraday's Law of Induction
 |
|
|
| Concepts | Meaning | |||||
|
The Inducecd Electric Field
|
||||||
 |
The Line Integral Over a Closed Path C
If we make the pieces infinitely small (N -> ∞) , then the summation becomes a line integral
|
|||||
 |
The Induced Electric Field Circulation
|
|||||
 |
The Rate of Change of Magnetic Flux
|
4. Ampere-Maxwell's Law
 |
 |
| Concepts | Meaning | |||
 |
The Induced Magnetic Field Circulation An electric current or a changing electric flux through a surface produces a circulating magnetic field around any path that bounds that surface. The current and the induced magnetic field follow the right-hand rule as shown below.
|
|||
|
The Permeability of Free Space
|
||||
|
The Enclosed Electric Current
|
||||
 |
The Rate of Change of Electric Flux (Displacement Current) This term is the electric flux analog of the changing magnetic flux term in Faraday's law of induction as mentioned above. Faraday's law of induction says that a changing magnetic flux through any surface induces a circulating electric field along a boundary path. This part was added by Maxwell into the original Ampere's equation. It says that a changing electric flux through a surface should induce a circulating magnetic field around a boundary of that surface. This term solved the capacitor charging/discharging paradox which cannot be counted as an ecnlosed electric current. In the following figure, should ic be considered an enclosed current? No. Instead we should count the electric field flux change between the plates of the capacitor (Q and -Q). This electric flux change happens when the capacitor is charging or discharging.
This electric flux change is calculated by integrating electric field E over the bulging surface which is bounded by the closed path C and then take the direct direvative over time (t). |
Differential Forms
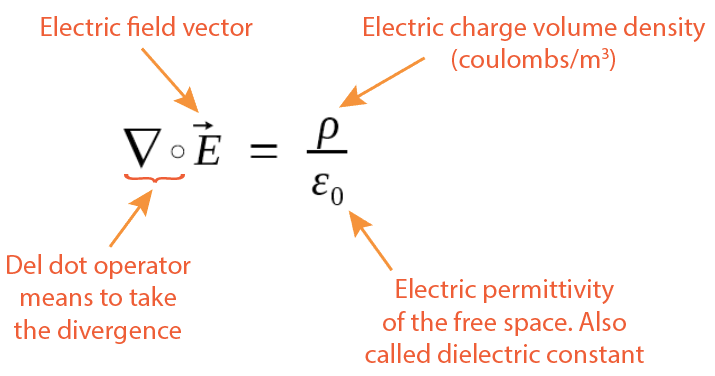
1. Gauss's Law for Static Electric Field
 |
|
| Concepts | Meaning | |||
|
Nabla - the Del (Gradient) Operator The nabla symbol is a mathematical operator (just like the square root symbol). It means to take derivatives of the quantity following it which is the quantity's gradient. In Cartesian coordinate system, the Del operator is defined as:
where |
||||
|
Del Dot - The Divergence Operator
Divergence is a scalar quantity (not a vector). But the field that it operates on is a vector. Flux is defined over an area, while divergence is defined at individual points, don't confuse them. Divergence is the limit of flux through an infinitesimal surface surrounding the point as defined below.
|
||||
| ρ |
Charge volume density at one point, its unit is coulombs / meter3 |
|||
|
The Divergence of the Electric Field In Cartesian coordinate, the electric field vector can be decomposed into three components.
According to the definition of the del dot operator, we then have:
Thus, the divergence of an electric field is the sum of
|
2. Gauss's Law for Static Magnetic Fields
 |
|
3. Faraday's Law of Induction
 |
|
| Concepts | Meaning | |||||
|
Del Cross - the Curl Operator You get the curl of the point of interest in a vector field A by following the steps below:
The curl of a vector field is a point function and it measures how how much of the vector A swirls around the point in question. The curl of a vector field is another vector field, just like any cross product. In Cartisian coordinates, curl is calculated by doing partial derivates expressed as a determinant:
Each component of the curl of A indicates the tendency of the field to rotate around the respective axis x, y, z. |
||||||
|
Curl of the Electric Field Charge Based Fields: Charge based electric fields diverge from the points of positive charge and converge to points of negative charge. This type of fields do not circulate back on themselves and their curls are zero at every point. Induced Fields: Induced electric fields by changing magnetic fields are very different from charge based electric fields. Induced fields circulate back onto themselves and have no origination or termination points. Thus induced electric fields have curl. The faster the magnetic field changes, the larger the curl of the induced electric field.
|
4. Ampere-Maxwell's Law
 |
|
In an static electric field, the divergence at one point equals to the electric charge volume density ρ at that point divided by ε0. The physical meaning is: A circulating magnetic field is produced by an electric current and/or by an electric field that changes with time. |
| Concepts | Meaning | ||||
|
The Curl of the Induced Magnetic Field All magnetic fields circulate back upon themselves, and it curl is non-zero at exact the locations through which an electric current is flowing or an electric field is changing. Just because the field appears to curve doesn't mean that the curl is non-zero everywhere! This is a common mistake. Look at the picture below.
It looks like the paddlewheel would rotate clockwise owing to the curvature of the field. However, the downward curvature of the field is offset by the weakening of the field with the distance from the center of curvature. The upward-downward push is exactly compensated by the weaker-stronger push and the paddlewheel does not turn. The curl is zero at this location even though the field lines are curved! The magnetic field may be curved at many locations, but only at points where electric current is flowing or the electric flux is changing that the curl is non-zero. |
|||||
 |
The Displacement Current Density Displacement current density has the units of electric current density (Amps/meters2), and it has an associated magnetic field just as actual current do. However, displacement current doesn't represent an actual current of moving charges, but a time-varying electric field, it is the rate of change of electric field with time. In dielectric materials (as opposed to vacuum), displacement current also has a contribution from slight displacement of bounded charges (which is called dielectric polarization). The displacement current term was a crucial addition to Ampere's Circuital Law that completed Maxwell's equations and units electricity, magnetism and optics into one single unified electromagnetics theory. Adding this term (changing electric field as a source of the magnetic field) extended Ampere's law to time-dependent fields by eliminating the inconsistency with the principle of conservation of charge. The key concept here is that a changing electric field produces a changing magnetic field even when no charges are present and no physical current flows. Through this mechanism, electromagnetic waves (optical waves included) can propagate through a perfect vacuum, as changing magnetic fields induce electric fields, and changing electric fields induce magnetic fields. |
||||
|
The Conduction Electric Current Density The electric current density is defined as the vector current flowing through a unit cross-secional area perpendicular to the direction of the current. Thus it has a unit of amperes per sqare meter (A/m2). The electric current density in Ampere-Maxwell law includes all currents, including the bound current density in magnetic materials.
If the number density of charge carriers are n and the charge per carrier is q, then the amount of charge passing through a unit area perpendicular to the flow per second is: Total current I vs current density J: If J is uniform over a surface S:
If J is not uniform:
|